The k-nearest neighbors (k-NN) search is a fundamental operation in high-dimensional data processing, crucial for information retrieval, machine learning, and recommendation systems. This research introduces a novel selective vector replication method significantly enhancing k-NN search performance. By focusing on boundary vectors—those whose nearest neighbors span multiple clusters—we address the fundamental challenge where traditional clustering disperses nearest neighbors across multiple partitions. Our method formulates vector replication as an optimization problem that balances recall improvement against computational costs, leading to a practical solution that enhances both recall and query efficiency. Experimental results demonstrate substantial improvements over existing approaches, achieving up to 62.2% reduction in vectors accessed while maintaining 0.95 recall on large-scale datasets. These findings confirm that selective replication of boundary vectors captures most potential efficiency gains with modest storage overhead.
The k-nearest neighbors (k-NN) query stands as a cornerstone operation in modern computing, playing a crucial role across diverse applications, including information retrieval, machine learning, retrieval-augmented generation, and recommendation systems. However, executing these queries efficiently in high-dimensional spaces remains challenging due to the curse of dimensionality, which fundamentally impacts both the effectiveness of distance metrics and the performance of vector indexing and search methods.
Many vector indexing systems have evolved to address these challenges through approximate k-NN queries, primarily utilizing partitioning or clustering techniques. These methods organize datasets into manageable subsets, effectively reducing the search space and improving query efficiency. Clustering has become central to numerous approaches, forming the foundation for inverted file (IVF)–based indexing and quantization methods, enabling scaling and parallelization of vector indices. Methods such as Product Quantization (PQ), Hierarchical Navigable Small World (HNSW), and DiskANN partition datasets to allow independent indexing and searching. Recent solutions such as SPANN and VexLS have further advanced the field by distributing vectors across multiple storage units or processes, enabling parallel data access and query processing.
However, a fundamental challenge persists: clustering high-dimensional vectors into well-separated clusters remains problematic. Traditional clustering algorithms typically optimize for representation quality or cluster cohesion, which may not align with the specific requirements of k-NN search. Consequently, the nearest neighbors of a query vector are often dispersed across multiple clusters, leading to reduced recall and increased query costs due to the necessity of accessing various clusters during the search process.
We introduce a selective vector replication method that optimizes clustering outputs for k-NN recall and search performance. Our approach functions as a post-processing step, seamlessly integrating with existing clustering or partitioning techniques. By identifying boundary vectors—those whose k-nearest neighbors reside in different clusters—we selectively replicate a subset of their closest neighbors into the corresponding clusters. This strategy improves k-NN recall while controlling the number of vectors accessed during queries.
Our experimental results demonstrate significant improvements over several baselines, including standard clustering without replication, soft clustering heuristics, and existing replication strategies like those used in SPANN. On a dataset of one million vectors clustered into 100 clusters, our method improved recall from 0.87 to 0.96 while accessing the same amount of data during queries. These findings confirm that selective replication of boundary vectors captures most potential efficiency gains with modest storage overhead.
In this paper, we contribute a novel selective replication method that enhances k-NN recall and search performance by focusing on boundary vectors. The replication selection can be seen as an optimization problem that maximizes a utility function balancing recall improvement and vector access cost. By prioritizing candidate vectors based on their frequency of appearance in the nearest neighbor lists of boundary vectors, we effectively identify those critical for enhancing recall. We develop an efficient approximation algorithm based on the set cover problem, incorporating diminishing returns and leveraging its submodular property to achieve strong performance guarantees. These contributions, supported by comprehensive experiments, confirm the practical applicability of our approach to large-scale datasets.
We use the terms partitioning and clustering interchangeably to refer to the overall process of splitting the data into subsets. Clustering typically refers to a special type of partitioning that uses similarity as the criteria for partitioning.
Various clustering methods, including soft clustering approaches, have been developed to assign vectors to multiple clusters. Soft clustering allows vectors to belong to multiple clusters with varying degrees of membership, capturing the inherent ambiguity in data assignment. These methods are typically designed in unsupervised learning and data mining, where the primary objective is to optimize representation quality and cohesion, similar to k-means clustering.
For approximate k-NN search, the primary goals shift towards maximizing recall and minimizing query time. Replication methods in recent solutions, such as SPANN, also follow approaches that prioritize representation quality. However, the replication is guided by distance-based data distribution characteristics rather than being directly optimized for k-NN recall and query efficiency.
A more aligned approach for k-NN search would be replicating the k-nearest neighbors of all possible query vectors within a cluster. While minimizing the clusters necessary to probe, this strategy may lead to excessively large overhead storage, increasing the number of vectors that need to be processed during queries.
We formulate the problem as a multi-objective optimization task to address these challenges. The dual objectives are to improve recall and minimize the number of vectors accessed during queries. By treating these objectives simultaneously, we aim to find an optimal balance that enhances k-NN search performance without incurring excessive computational costs.
This section introduces the background and key concepts that underpin the problem of enhancing k-nearest neighbor (k-NN) recall in similarity search through selective vector replication.
Consider a dataset X = {x₁, x₂, ..., xₙ} in a d-dimensional space. The dataset is partitioned into K disjoint clusters C = {C₁, C₂, ..., Cₖ} such that:
Each cluster Cᵢ is associated with a centroid μᵢ, which is typically the mean of the vectors in Cᵢ. Clustering facilitates efficient similarity search by allowing queries to be processed within a subset of the data, reducing computational overhead. A query vector q is assigned to a cluster Cᵢ based on a proximity criterion, such as minimal distance to cluster centroids:
The search for nearest neighbors of q is then confined to Cᵢ, leveraging the clustering structure to improve efficiency. Multiple clusters are typically accessed to improve the recall of the results.
For a given vector x ∈ X, let Nₖ(x) denote its set of k-nearest neighbors in X \ {x} under a distance metric d(·,·). The k-NN search aims to find, for each query q, the set Nₖ(q) of k data points in X closest to q. When the search is restricted to a single or small number of clusters, the retrieved neighbors Nₖ^(Cᵢ)(q) may not include the true nearest neighbors if they reside outside Cᵢ. We define recall as the fraction of the true nearest neighbors that are successfully retrieved:
The overall recall is the average recall over all queries.
The search time in k-NN queries is primarily determined by the number of vectors accessed and processed. In disk-based systems, the dominant cost arises from the size of data read from disk, while in in-memory systems, it depends on the number of vectors processed in memory. Our approach aims to improve search time by reducing the number of vectors accessed during queries through selective vector replication. We enhance recall by increasing the likelihood that a query's nearest neighbors exist within the clusters accessed while minimizing search time.
Our objective is to select, for each cluster Cᵢ, a set of vectors Tᵢ to replicate into Cᵢ to maximize recall while minimizing search time. We aim for Tᵢ to consist of vectors most likely to improve recall when replicated into clusters where they do not originally belong.
We define the set of boundary vectors in cluster Cᵢ as those vectors whose k-nearest neighbors include vectors from other clusters:
Boundary vectors indicate regions where clustering may cause a loss in recall, as their nearest neighbors cross cluster boundaries.
We focus on replicating vectors frequently appearing in the k'-nearest neighbor lists of boundary vectors. This targets replication where it most effectively improves recall per unit of replication. If there is no specific query workload, we consider the dataset itself as the query set.
Let Nₖ'(x) denote the set of k'-nearest neighbors of x in X \ {x}, where k' ≥ k allows us to consider a broader set of candidates. We define the candidate set for cluster Cᵢ as:
To quantify the importance of each candidate vector y ∈ Yᵢ, we introduce the frequency score:
This score measures how often y appears in the neighbor lists of boundary vectors in Cᵢ, indicating the potential impact on recall when y is replicated into Cᵢ.
We define a utility function for each cluster Cᵢ that balances recall improvement against the cost of vector access:
where R(Tᵢ) is the expected recall with replication set Tᵢ, V(Tᵢ) = |Cᵢ| + |Tᵢ| is the total number of vectors accessed during query processing in Cᵢ after replication, and α, β > 0 are parameters weighing recall improvement against the cost of vector access.
Computing R(Tᵢ) exactly is computationally intensive. To make the problem tractable, we approximate the expected recall:
where R₀ is the baseline recall without replication, and γ is a scaling factor normalizing the contribution of the frequency scores.
Substituting this approximation into the utility function and focusing on terms dependent on Tᵢ, we obtain:
where α' = αγ and β' = β. The constant term can be ignored for optimization purposes.
We also introduce a replication capacity constraint Nᵢ, representing the maximum number of vectors that can be replicated into cluster Cᵢ, reflecting storage and efficiency considerations. Our optimization problem is to select Tᵢ ⊆ Yᵢ that maximizes:
This problem resembles a knapsack problem, which is NP-hard. Therefore, we seek efficient approximation algorithms to solve it, as detailed in the subsequent sections.
In this section, we present our selective replication method that simultaneously improves recall and processing costs. Assuming vectors are sparsely distributed across clusters, for any query set Q and partition P = {C₁, ..., Cₚ}, there exists a replication set of size κ ≪ n(p - 1) ensuring each query has at least one of its k-nearest neighbors within its assigned cluster. In the absence of a query set, it is customary to use the dataset itself to train or evaluate index structures.
Identifying these optimal κ replications directly requires exhaustive nearest neighbor computations. To circumvent this, we frame replication selection as a set cover problem. For each cluster Cᵢ, its boundary vectors Bᵢ, and candidate vector y ∉ Cᵢ, we define:
where each Sᵧ represents boundary vectors whose recall would improve by replicating y into Cᵢ. Note that fᵢ(y) = |Sᵧ|, connecting the frequency score defined earlier to the size of the coverage sets in the set cover formulation.
Given δ ∈ (0,1) and the minimal cover size κ, sampling
boundary vectors uniformly at random from Bᵢ and applying a greedy set cover algorithm yields a replication set S that:
Leveraging this lemma, we sample a subset B̃ᵢ ⊆ Bᵢ of size s. To ensure robustness against sampling variance, we compute an expanded set of k'-nearest neighbors for each sampled vector using approximate search, forming the candidate set:
Our objective is to select a subset Tᵢ ⊆ Yᵢ that maximizes the coverage of B̃ᵢ while keeping |Tᵢ| small. This is equivalent to finding a set cover of B̃ᵢ using the sets {Sᵧ | y ∈ Yᵢ}.
We apply the greedy algorithm for set cover, which iteratively selects the candidate vector that covers the largest number of uncovered sampled boundary vectors. At each iteration, we select
where B̃ᵢ' is the set of uncovered sampled boundary vectors.
Input: Boundary set Bᵢ, sample size s = O(κ log² |Bᵢ|/δ), replication budget Nᵢ
Output: Replication set Tᵢ
1. Sample B̃ᵢ ⊆ Bᵢ uniformly at random, |B̃ᵢ| = s
2. Compute k'-nearest neighbors for each x ∈ B̃ᵢ, forming Yᵢ
3. Initialize Tᵢ ← ∅, B̃ᵢ' ← B̃ᵢ
4. While B̃ᵢ' ≠ ∅ and |Tᵢ| < Nᵢ:
4.1 Select y* = argmax_{y ∈ Yᵢ} |Sᵧ ∩ B̃ᵢ'|
4.2 Tᵢ ← Tᵢ ∪ {y*}
4.3 B̃ᵢ' ← B̃ᵢ' \ Sᵧ*
4.4 Remove y* from Yᵢ
5. Return Tᵢ
This approach effectively solves the optimization problem defined earlier by approximating the maximization of the utility function through set cover, connecting our frequency-based selection to a well-studied combinatorial optimization problem. The algorithm achieves an O(log |Bᵢ|)-approximation to the optimal cover size while requiring only O(ndκ log² |Bᵢ|) distance computations in d dimensions.
Algorithm 1 achieves an O(log |Bᵢ|)-approximation to the optimal cover size while maintaining the storage constraint |Tᵢ| ≤ Nᵢ.
The proof follows from the submodularity of the coverage function and the standard analysis of the greedy set cover algorithm. The sampling approach ensures we can efficiently process large-scale datasets while maintaining strong theoretical guarantees.
Building upon our selective replication strategy, we introduce a cost model to balance recall improvement with query costs. Let F(k) denote the cumulative probability of finding the nearest neighbor within the top k clusters, and let G = F⁻¹ be its inverse function. Without replication, achieving a target recall Rₜₐᵣᵧₑₜ requires probing k* = G(Rₜₐᵣᵧₑₜ) clusters.
Introducing a replication factor r = |T|/n, where |T| is the size of the replication set and n is the total number of vectors, adjusts the expected recall for a query q to:
This accounts for the probability that the nearest neighbor is found within the replicated set T with probability r or within the top k clusters with adjusted probability (1-r)F(k). To maintain the target recall Rₜₐᵣᵧₑₜ, we adjust the number of required probes to:
Let B denote the number of clusters, and p(k) represent the probability of accessing the k-th cluster. The total number of vectors accessed during query processing is given by:
where n/B is the average number of vectors per cluster, and (1-p(1))r accounts for replication overhead in accessing additional vectors.
For data following a Zipfian distribution with p(k) ∼ 1/k, the query cost simplifies to:
Building on our set cover formulation with coverage scores s(y) = |Sᵧ|, we model recall using an exponential function to capture the natural diminishing returns of vector replication:
where R₀ is baseline recall and λ controls the diminishing returns rate. The exponential form ensures the recall improvement is bounded and provides a single parameter λ to control the rate of saturation.
The total cost C(T) combines storage and query overhead:
From our optimization framework, we aim to maximize the net utility, balancing recall improvement against costs:
where α and β determine the recall-cost trade-off. The marginal utility of adding a vector y to the replication set T is defined as:
where S = Σᵧ'∈T s(y') is the current coverage score.
Input: Candidate set Y, coverage scores s(y), parameters α, β, λ
Output: Replication set T
1. Initialize T ← ∅, S ← 0
2. While True:
2.1 r ← |T|/n // Current replication factor
2.2 If r ≥ r* or V(T) > V(T \ {last added}):
Break
2.3 Compute ΔR(y) and ΔC(y) for each y ∈ Y \ T
2.4 Select y* = argmax_{y ∈ Y \ T}[α·ΔR(y) - β·ΔC(y)]
2.5 If α·ΔR(y*) - β·ΔC(y*) ≤ 0:
Break
2.6 Update T ← T ∪ {y*}
2.7 Update S ← S + s(y*)
3. Return T
This cost-aware selection algorithm extends our earlier utility maximization by explicitly incorporating storage and query costs, allowing for a more nuanced trade-off between recall improvement and resource consumption.
We conduct experiments on three large-scale datasets representing different real-world vector search scenarios: LAION10M containing 10 million 768-dimensional image embeddings, COHERE5M with 5 million 768-dimensional Wikipedia articles embeddings, and GIST1M comprising 1 million 960-dimensional GIST descriptors. These datasets exhibit diverse characteristics in terms of dimensionality, size, and data distribution.
For clustering granularity, we use k-means with different numbers of clusters tailored to each dataset's size: 1000 clusters for LAION10M, 500 for COHERE5M, and 100 for GIST1M. All experiments were conducted on an AWS p3.16xlarge EC2 instance with 488GB RAM and 8 NVIDIA V100 GPUs, though our method primarily utilizes CPU resources for both indexing and search, and can run on the majority of common hardware.
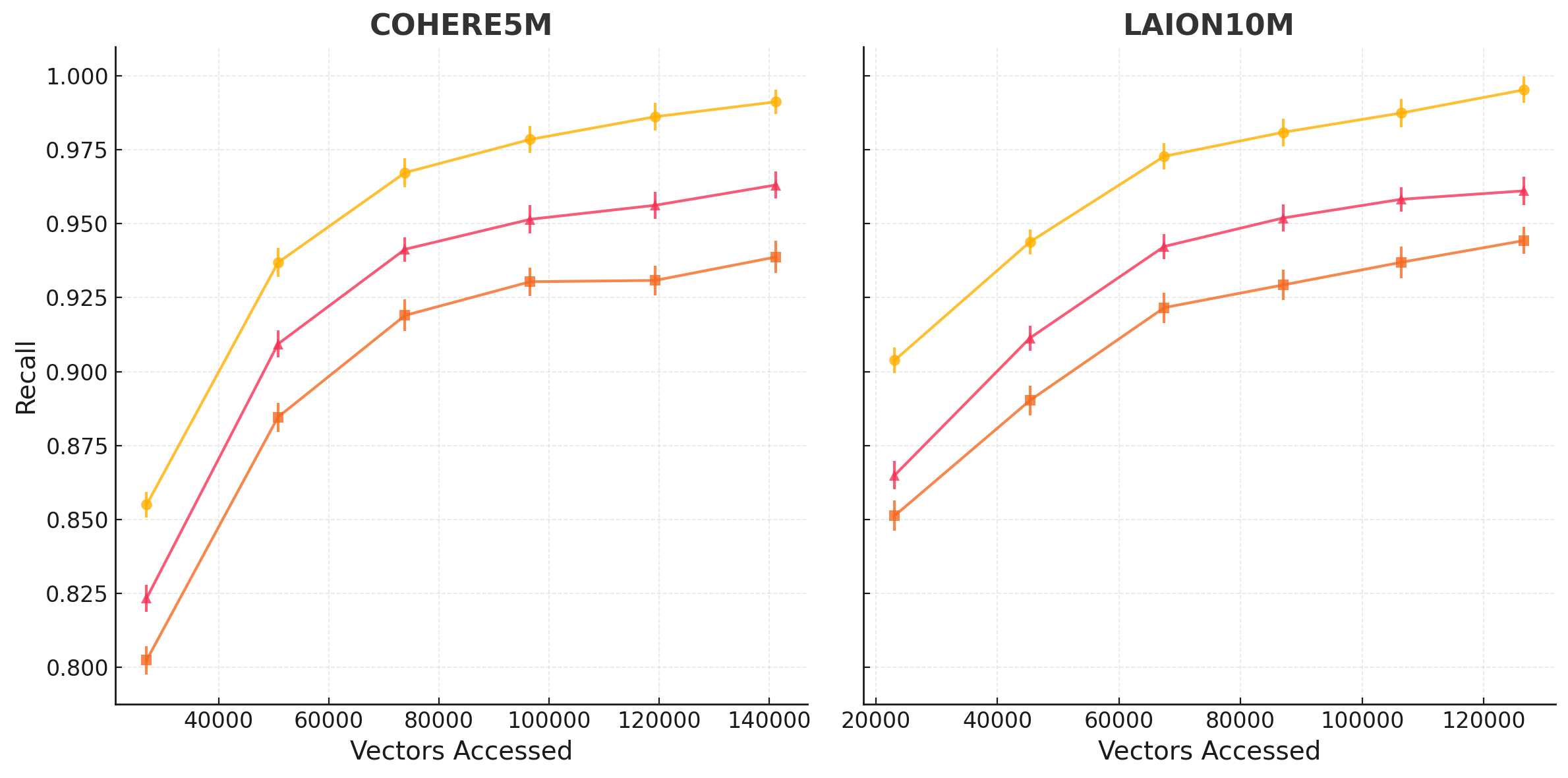
Figure 1 demonstrates the effectiveness of our selective vector replication method compared to the baselines across LAION and COHERE embeddings, with all methods normalized to use 100% storage overhead. For LAION10M, at this fixed storage budget, our method achieves 0.96 recall while accessing 97K vectors, compared to 193K vectors needed by the baseline approaches - a 49.7% reduction in vectors accessed.

The performance gains are consistent across datasets of different characteristics. On COHERE5M, with text embeddings of equal dimensionality, our method reduces vectors accessed by 62.2% (from 196K to 74K vectors) to achieve 0.95 recall. The performance improvement is particularly pronounced in the high-recall regions (>0.90), where identifying the true nearest neighbors becomes increasingly challenging.
Figures 2 and 3 illustrate how boundary vector coverage impacts the number of vectors accessed to achieve target recall levels. Coverage, ranging from 0.1 to 0.7, represents the fraction of boundary vectors whose k' nearest neighbors are replicated to their respective clusters.

For COHERE5M, to achieve a fixed recall target of 0.95, increasing coverage from 0.1 to 0.5 reduces vectors accessed from approximately 120K to 60K. Coverage beyond 0.5 yields diminishing efficiency gains - a pattern consistent with our theoretical analysis of set cover optimization.
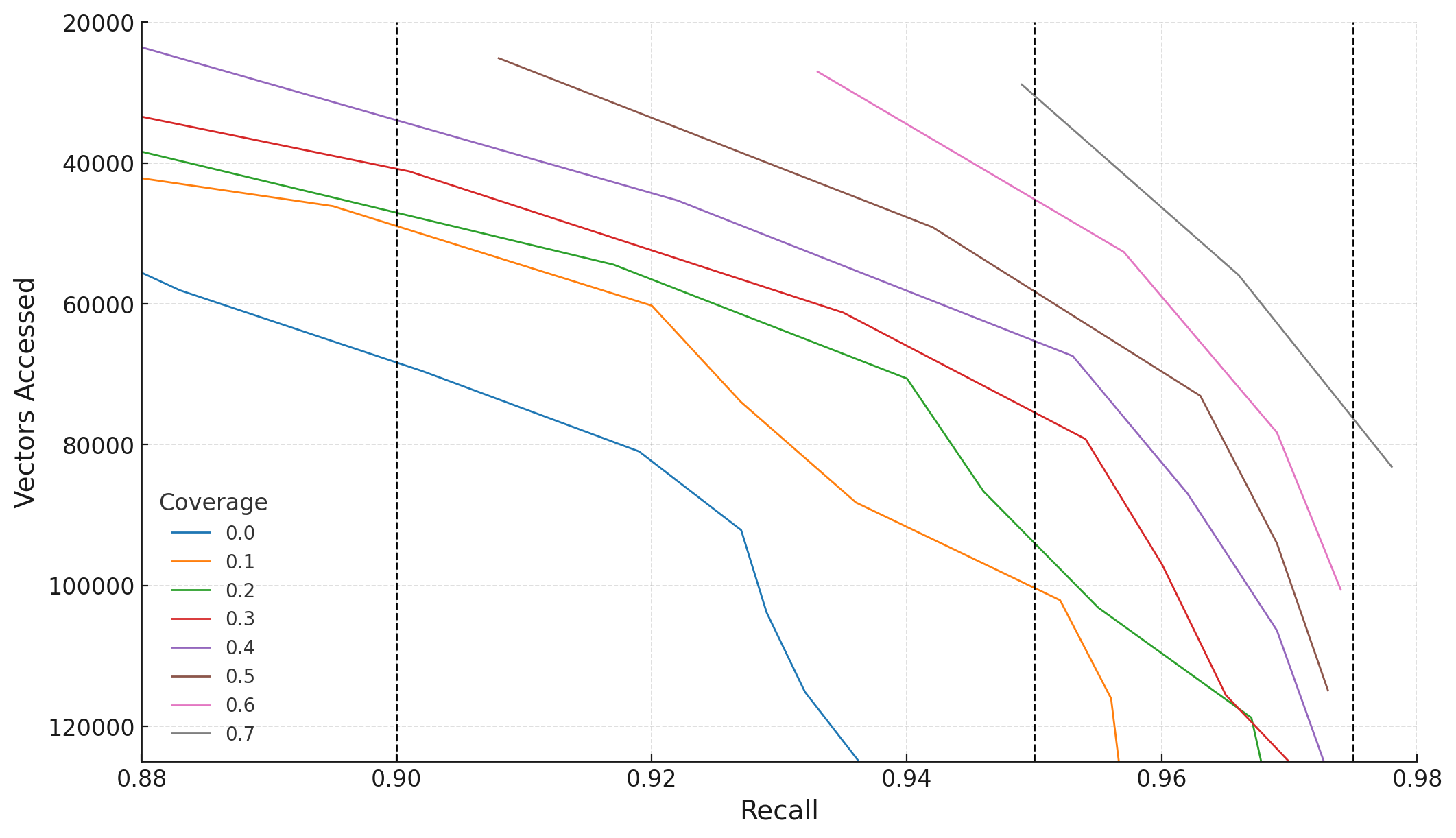
Figure 4 illustrates the marginal improvement behavior of our replication strategy as coverage increases on the GIST dataset, revealing distinct operating regions. In the initial region (0-10% replication), we observe major improvements where both recall improves sharply and the number of vectors accessed decreases.
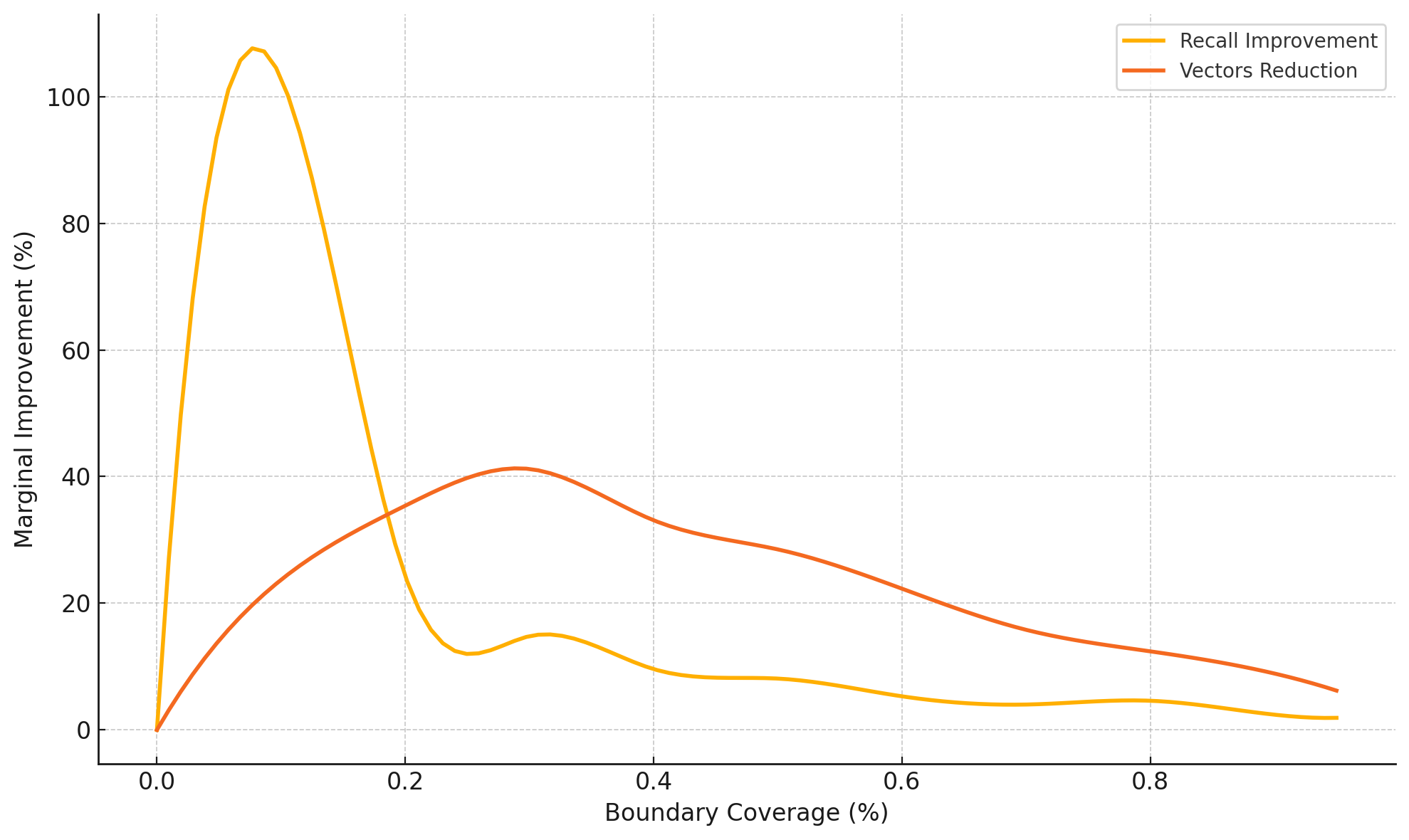
Beyond 10% replication, we enter a trade-off region where marginal recall improvements diminish. The vector reduction curve shows that the efficiency gains from replication decline steadily after the 30% mark. This pattern aligns with our cost model analysis, which predicted such diminishing returns.
Figure 5 demonstrates the Pareto frontier achieved by our selective replication method across different operating points. Each point on the curve represents a different configuration of replication factor and number of probes, with the frontier line showing the optimal trade-off between recall and vectors accessed.
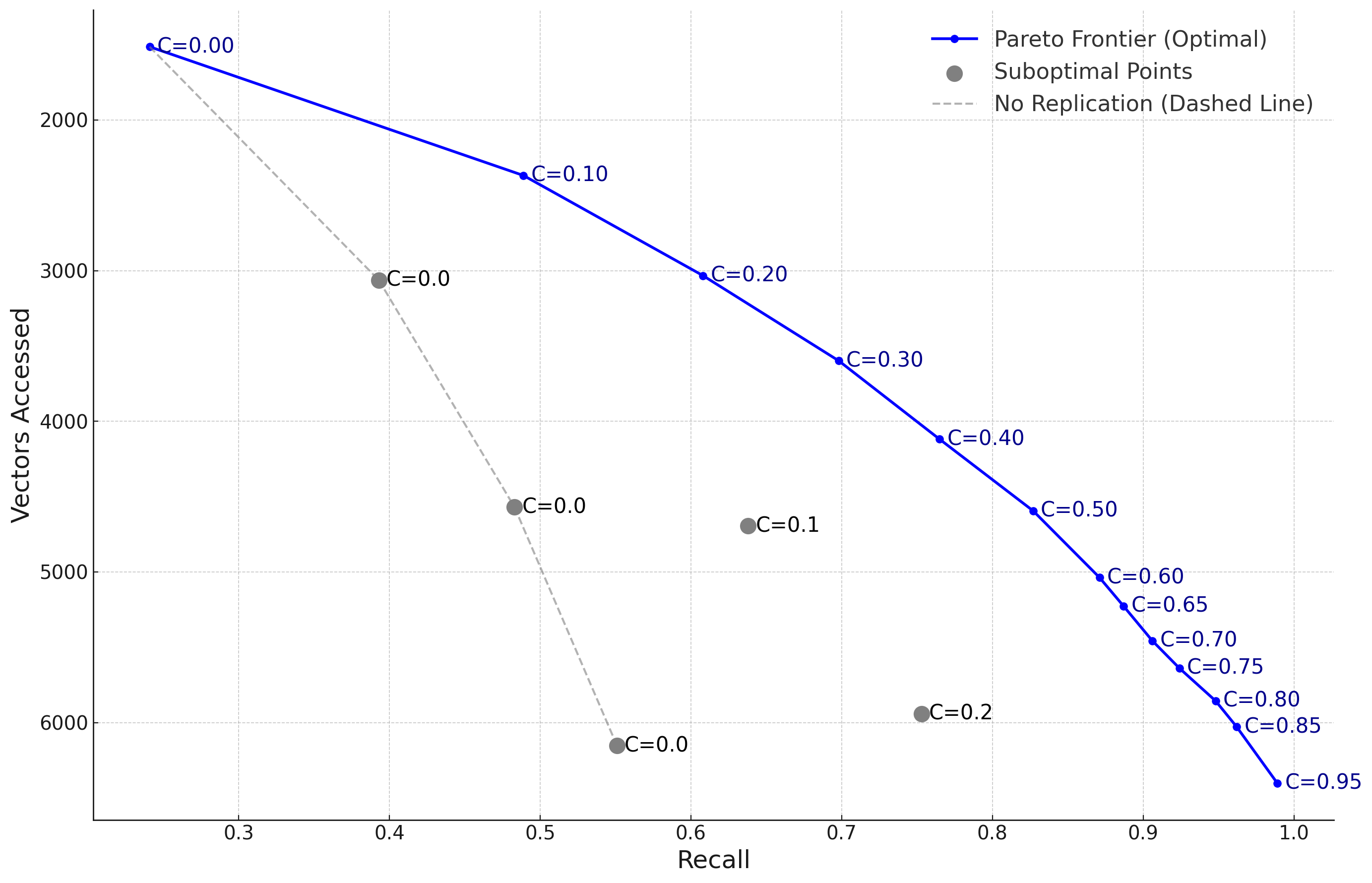
The results validate our theoretical analysis, which predicted the existence of these Pareto-optimal configurations. At C=0.3, we achieve 0.95 recall while accessing only 35% of the vectors required by the baseline approach with no replication. As coverage increases to C=0.5, recall improves to 0.97 but with diminishing efficiency gains, aligning with our utility function model.
The practical implications of this analysis suggest that practitioners should focus on the steep initial portion of the Pareto curve (0.2 ≤ C ≤ 0.4), where recall improvements are most cost-effective. This region provides the best balance between storage overhead, computational efficiency, and recall performance, achieving 95-97% of the maximum possible recall while keeping vector access costs to a practical minimum.
We have introduced a selective vector replication method that significantly enhances the recall and query performance of approximate nearest neighbor (k-NN) search in high-dimensional spaces. By focusing on boundary vectors—those whose nearest neighbors reside in different clusters—we address the fundamental challenge where traditional clustering disperses nearest neighbors across multiple clusters, degrading recall and increasing search costs. Our method formulates vector replication as an optimization problem that maximizes a utility function balancing recall improvement against the cost of vector access, leading to a combinatorial optimization solution based on the set cover problem.
Through theoretical analysis, we confirm the optimality of selecting boundary vectors for replication and provide approximation guarantees for our set cover-based approach. By incorporating diminishing returns into the utility function and leveraging submodularity properties, we achieve efficient approximation solutions with strong performance guarantees. Empirical evaluations on large-scale datasets demonstrate substantial improvements over existing baselines, not only enhancing recall but also reducing the number of vectors accessed during queries. These results confirm that selective replication of boundary vectors captures the majority of potential efficiency gains with modest storage overhead.
One limitation of our current approach is the assumption of uniform costs when covering the query set, whereas, in practice, the cost of covering subsets of queries within the same cluster differs from covering those across different clusters. This suggests an extension to our method by considering a cost model where coverage depends on cluster membership. By prioritizing neighbor vectors that cover the most queries within the same cluster—measured by the cluster-wise reverse nearest neighbor (RNN) size—we can further minimize the replication factor while maintaining high recall.
Incorporating diversity into the replication process is a possible valuable extension. By selecting a diverse sample of boundary vectors to represent cluster boundaries and choosing a diverse set of neighbors for each boundary vector, we can reduce redundancy and improve query efficiency. Instead of replicating only the top-k neighbors, we can consider a larger set and select a diverse subset to replicate. This strategy brings in vectors from clusters spread across the data space, reducing the likelihood of redundant vector accesses during queries.
Jointly designing replication and query processing strategies can further enhance performance. While our method optimizes replication, accessing only the closest clusters during queries may result in redundant vector accesses due to replicated vectors from neighboring clusters. By diversifying the replication process and potentially defining a novel optimization setting—such as a Diverse Bi-Directional Set Cover—we aim to achieve diverse coverage of replicated vectors, avoiding redundancy and improving efficiency.
We also explore the concept of partially covering the query set to maximize recall, akin to strategies used in Determinantal Point Processes. By using the k'-nearest neighbors set as a proxy to diversely cover the query space, we can select a representative subset of vectors for replication without directly sampling from the query set. This method allows us to achieve high recall with minimal vectors accessed per query, particularly when replication costs are negligible. However, determining the optimal value of k' is challenging, as it influences the balance between recall improvement and the number of vectors accessed.
In summary, our selective vector replication method offers a practical and theoretically grounded solution to enhance k-NN search performance in high-dimensional spaces. By strategically replicating vectors based on boundary analysis and optimization, we achieve significant improvements in both recall and query efficiency. The method's flexibility allows for various extensions, such as incorporating diversity and adjusting for cluster-specific costs, which can further enhance its applicability and performance. Future work will focus on exploring these extensions and addressing current limitations, aiming to develop a comprehensive framework for efficient and accurate similarity search in high-dimensional data.
Bezdek, J. C. (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. Springer Science & Business Media.
Li, J., Sun, W., Zhu, Y., Xiao, F., Li, H., Lin, Q., Luo, D., & Yang, J. (2020). SPANN: Highly Scalable Billion-Scale Approximate Nearest Neighbor Search. Proceedings of the VLDB Endowment, 13(9), 1359-1371.
Su, Y., Sun, Y., Zhang, M., & Wang, J. (2024). Vexless: A Serverless Vector Data Management System Using Cloud Functions. Proceedings of the ACM on Management of Data (SIGMOD), 2(3), 187:1-187:26.
Jégou, H., Douze, M., & Schmid, C. (2011). Product quantization for nearest neighbor search. IEEE Transactions on Pattern Analysis and Machine Intelligence, 33(1), 117-128.
Malkov, Y. A., & Yashunin, D. A. (2020). Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 42(4), 824-836.
Subramanya, A., Pendyala, R. P., Sabharwal, A., & Varma, M. (2019). DiskANN: Fast accurate billion-point nearest neighbor search on a single node. Advances in Neural Information Processing Systems, 32, 13745-13755.
Kulesza, A., & Taskar, B. (2012). Determinantal point processes for machine learning. Foundations and Trends in Machine Learning, 5(2-3), 123-286.
Schuhmann, C., et al. (2021). LAION-400M: Open Dataset of CLIP-Filtered 400 Million Image-Text Pairs. arXiv preprint arXiv:2111.02114.
MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1, 281-297.
Korte, B., & Vygen, J. (2008). Combinatorial Optimization: Theory and Algorithms (5th ed.). Springer.
Nemhauser, G. L., Wolsey, L. A., & Fisher, M. L. (1978). An analysis of approximations for maximizing submodular set functions—I. Mathematical Programming, 14(1), 265-294.